Author:
(1) Yuki Koto
Table of Links
- Abstract and Intro
- Genus-zero Gromov-Witten Theory
- Toric Bundles
- Lagrangian cones of Toric bundles
- Mirror theorem for a product of projectives bundles
- Mirror Theorem for Toric Bundles
- Appendix A. Equivariant Fourier Transformation and References
2. Genus-zero Gromov-Witten theory
In this section, we briefly recall the (torus-equivariant/twisted) genus-zero Gromov-Witten theory. We will introduce Gromov-Witten invariants, Givental Lagrangian cones and the quantum Riemann-Roch theorem.
2.1. Gromov-Witten invariant and its variants. We recall the definition of Gromov-Witten invariant. We also introduce an torus-equivariant version and a twisted version of it.




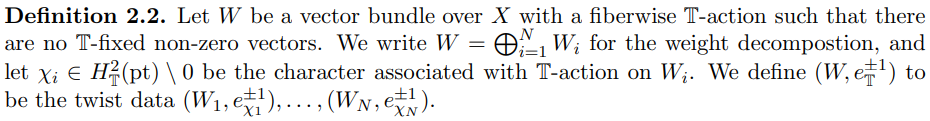




2.3. Quantum Riemann-Roch theorem and twisted theory. We introduce quantum Riemann-Roch theorem [9, Corollary 4], which relates twisted Givental cones via some transcendental operators. We also explain relationships between the Gromow-Witten theory of a vector bundle (resp. a subvariety) and that of a base space (resp. an ambient space) in terms of twisted theories. Note that we will use the material in this subsection only in Section 5.






This paper is available on arxiv under CC 4.0 license.

