Authors:
(1) Bobby He, Department of Computer Science, ETH Zurich (Correspondence to: bobby.he@inf.ethz.ch.);
(2) Thomas Hofmann, Department of Computer Science, ETH Zurich.
Table of Links
Simplifying Transformer Blocks
Discussion, Reproducibility Statement, Acknowledgements and References
A Duality Between Downweighted Residual and Restricting Updates In Linear Layers
5 FURTHER EXPERIMENTAL ANALYSIS
Having detailed all of our simplifications in Sec. 4, we now provide further experimental results of our simplified blocks in a range of settings, as well as details of the efficiency gains afforded by our simplifications. In the interest of space, additional experimental details can be found in App. D.
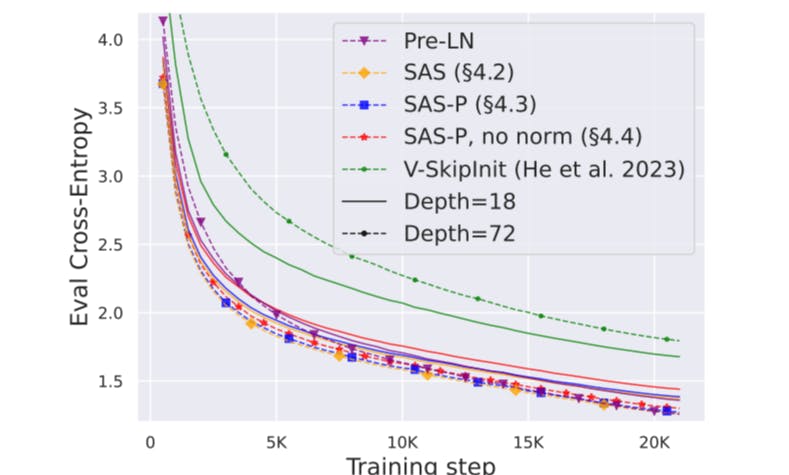
Depth Scaling Given that signal propagation theory often focuses on large depths, where signal degeneracies usually appear, it is natural to ask whether the improved training speeds of our simplified transformer blocks also extend to larger depths. In Fig. 6, we see that scaling depth from 18 to 72 blocks leads to an increase in performance in our models as well as the Pre-LN transformer, indicating that our simplified models are able to not only train faster but also to utilise the extra capacity that more depth provides. Indeed, the per-update trajectories of our simplified blocks and Pre-LN are near-indistinguishable across depths, when using normalisation.
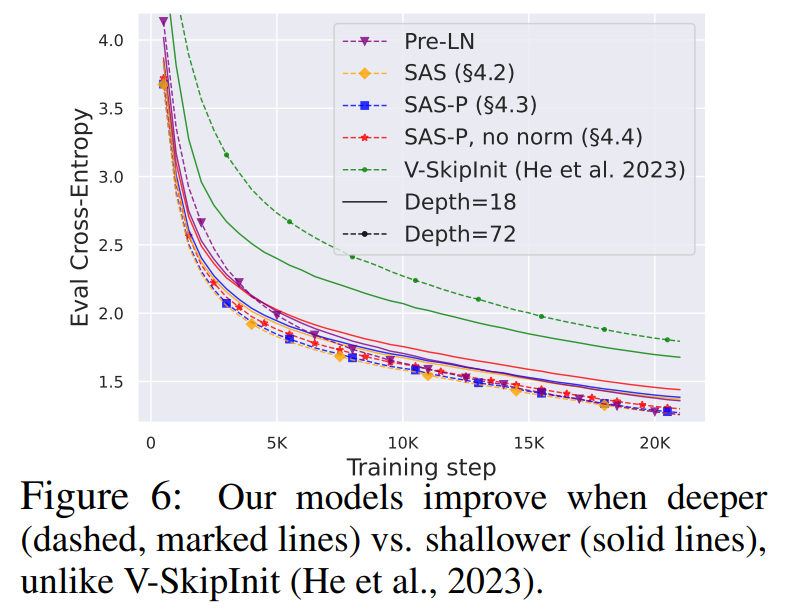
On the other hand, we see that Value-SkipInit (He et al., 2023) actually trains slower per update at depth 72 compared to 18 despite the increase in capacity and parameter count. Moreover, the gap in performance between Value-SkipInit and the other models increases with larger depth, which implies poor scalability of the previous method. We note that 72 blocks is already reasonably deep by publically-available modern standards (Hoffmann et al., 2022; Touvron et al., 2023).
BERT Next, we demonstrate our simplified blocks’ performance extends to different datasets and architectures besides autoregressive decoder-only, as well as on downstream tasks. We choose the popular setting of the bidirectional encoder-only BERT model Devlin et al. (2018) for masked language modelling, with downstream GLUE benchmark.
In particular, we adopt the “Crammed” BERT setup of Geiping & Goldstein (2023), which asks how well one can train a BERT model with a modest training budget: 24 hours on a single consumer GPU. The authors provide an architecture, data pipeline and training setup that has been optimised for this low resource setting. We note that the Crammed architecture uses the Pre-LN block, and describe other setup details in App. D. We plug-in our simplified blocks, keeping the existing optimised hyperparameters, besides tuning learning rate and weight decay.
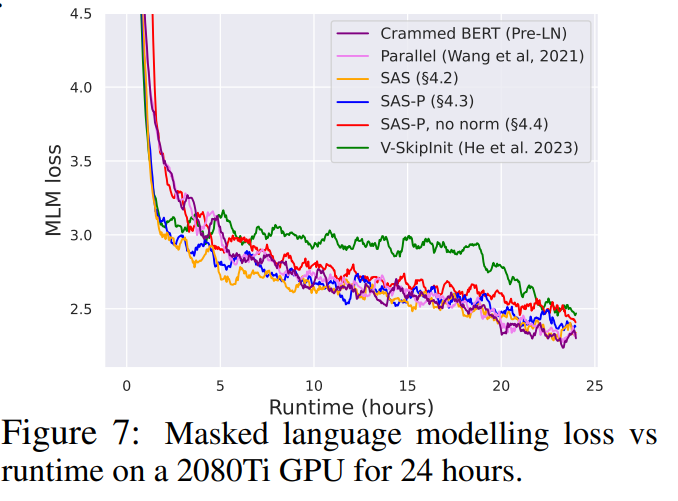
In Fig. 7, we see that our simplified blocks (especially with normalisation) match the pre-training speed on the masked language modelling task compared to the (Crammed) Pre-LN baseline within the 24 hour runtime. On the other hand, the removal of skip connections without modifying the values and projections (as in He et al. (2023)) once again leads to a significant loss of training speed. In Fig. 24, we provide the equivalent plot in terms of microbatch steps.
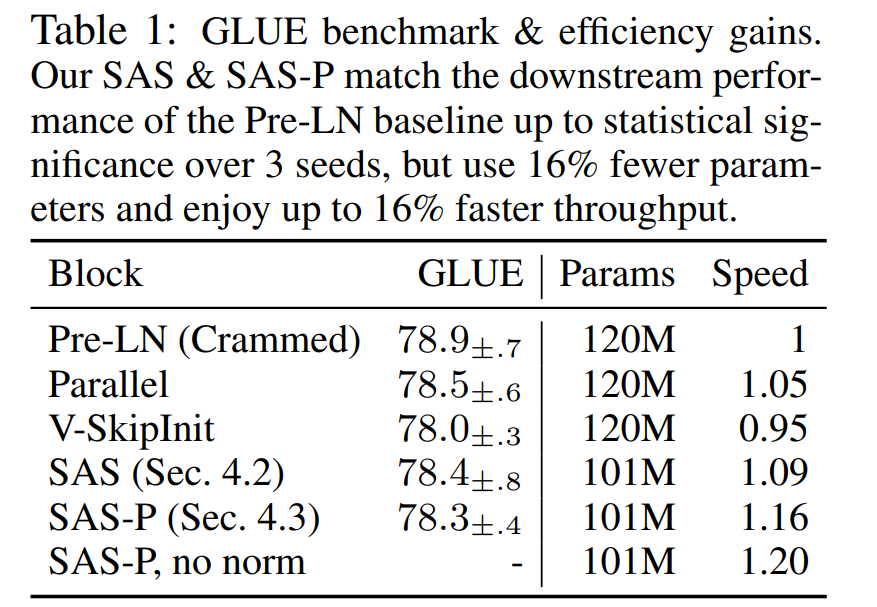
Moreover in Table 1, we find that our methods match the performance of the Crammed BERT baseline after finetuning on the GLUE benchmark. We provide a breakdown over the downstream tasks in Table 2. We use the same finetuning protocol as Geiping & Goldstein (2023) (5 epochs, constant hyperparameters across tasks, dropout regularisation) for a fair comparison. Interestingly, Value-SkipInit is largely able to recover from its poor pre-training in the fine-tuning phase. This, combined with the need for dropout when fine-tuning, suggests that factors besides pre-training speed are also important for fine-tuning. As the focus of our work primarily concerns training speed from random initialisations, we leave this to future work. Relatedly, we found removing normalisations (Sec. 4.4) to cause instabilities when fine-tuning, where a small minority of sequences in some downstream datasets had NaN values in the initial forward pass from the pre-trained checkpoint.
Efficiency Gains In Table 1, we also detail the parameter count and training speeds of models using different Transformers blocks on the masked language modelling task. We compute the speed as the ratio of the number of microbatch steps taken within the 24 hours of pre-training, relative to the baseline Pre-LN Crammed BERT. We see that our models use 16% fewer parameters, and SAS-P & SAS are 16% & 9% faster per iteration, respectively, compared to the Pre-LN block in our setting. We note that in our implementation the Parallel block is only 5% faster than the Pre-LN block, whereas Chowdhery et al. (2022) observed 15% faster training speeds, suggesting that further throughout increases may be possible with a more optimised implementation. Our implementation, like Geiping & Goldstein (2023), uses automated operator fusion in PyTorch (Sarofeen et al., 2022)
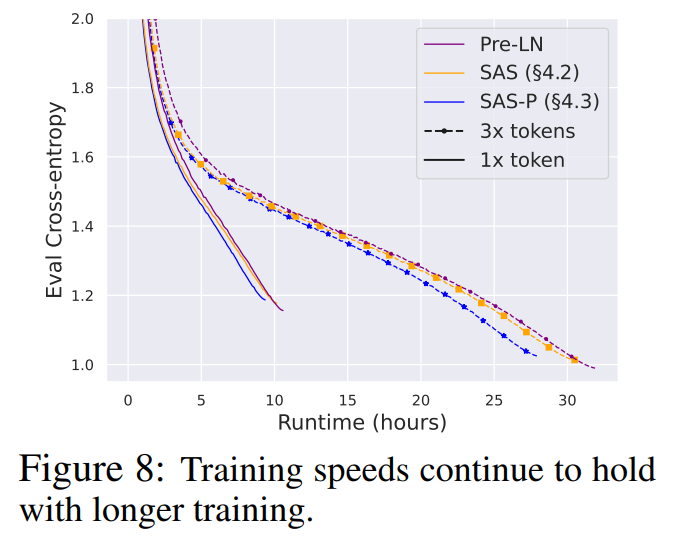
Longer training Finally, given the current trends of training smaller models for longer on more data (Hoffmann et al., 2022; Touvron et al., 2023), we investigate if our simplified blocks continue to match the training speeds of the Pre-LN block with longer training. To do this, we take our models from Fig. 5 on CodeParrot and train with 3× tokens. To be precise, we train for around 120K (rather than 40K) steps with batch size 128 and sequence length 128, which results in around 2B tokens. In Fig. 8, we do indeed see that our simplified SAS and SAS-P blocks continue to match or outer perform the PreLN block in training speed when trained on more tokens.
This paper is available on arxiv under CC 4.0 license.